本帖最後由 秦伊人 於 2022-11-14 09:14 編輯
(第三页)
b模数转换
历法数据(历数)来自何处?在《周髀》中对此问有答案:历数来自测量。自古有“立竿见影”之说,测日影确定历数是古历法的基本手段。“一丈之表”和“八尺之表”都是古人测影的工具,而“表”本身也是一个尺度,“表尺”对应日影,“圭尺”对应历法。在“八尺之表”的体系中,圭尺长度一丈二尺,为了换算方便,圭尺刻度取整数180格,一年日影两次掠过圭尺,计360格。用干支度量圭尺,360格折合六个干支长度。若每格对应一日,六个干支长度就可以每干支对应一日。
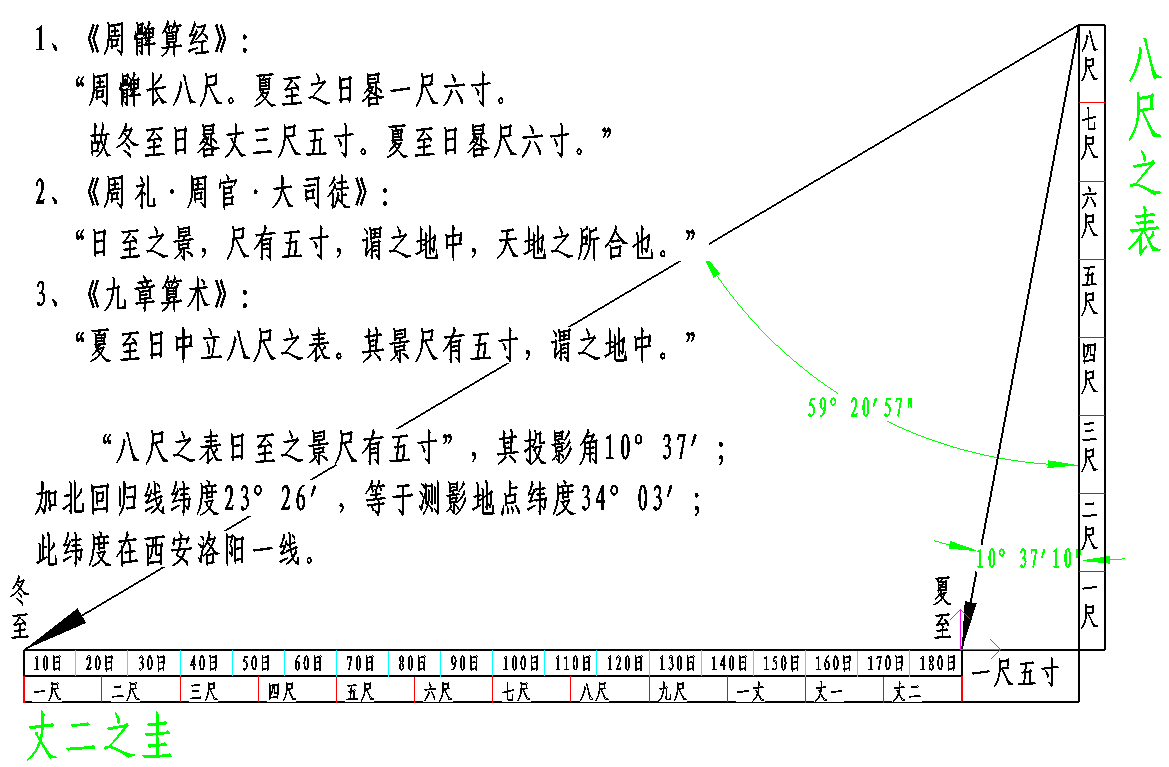
《尧典》将一年根据气候分成春、夏、秋、冬,所谓“四时”,合计天数366日;对“八尺之表”的360格,用366日修正,则每干支长度(六十干支日)再加一日。
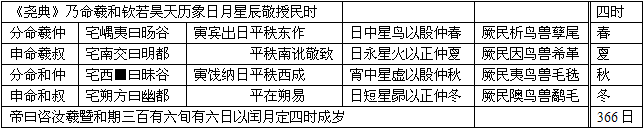
董作宾也说历法有三把尺子,这就是日尺、月尺、年尺,这三把尺子的数据:
1、气尺(年)(31+30)/2=30.5 (合阳历)12×30.5=366 2、癸尺(日)(30+30)/1=60.0 (合干支)06×60.0=360 3、朔尺(月)(30+29)/2=29.5 (合阴历)12×29.5=354
《尧典》的“十年四闰”历法:(124月为“闰周”)
历尺模型:(10×366=10×360+1×60=10×354+2×60=3660) 相当于:60条“气尺”=61条“癸尺”=62条“朔尺”
闰法:10×366 =(10×6×61) (60个气尺单位+0个癸尺单位) =(10×6×60+1×60)(60个癸尺单位+1个癸尺单位) =(10×6×59+2×60)(60个朔尺单位+2个癸尺单位) =3660
|